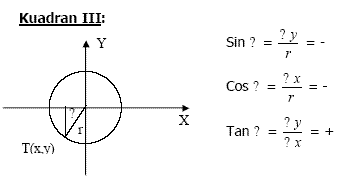TRIGONOMETRI

kita mulai terlebih dahulu dengan sebuah segitiga siku-siku , perhatikan gambar berikut :

Diketahui

sebuah sudut sebesar x derajat, dengan :

Sisi didepan x, sebesar b satuan disebut sisi depan (disingkat : DE))

Sisi disamping x, sebesar a satuan disebut sisi samping (disingkat : SA)

Sisi miring, sebesar c satuan disebut sisi miring (disingkat : MI)

sin x = b/c = perbandingan sisi depan(DE) dengan sisi miring (MI) —> dibaca : DEMI

cos x = a/c = perbandingan sisi samping (SA) dengan sisi miring (MI) —> dibaca : SAMI

tan x = b/a = perbandingan sisi depan(DE) deng

an sisi samping (SA) —> dibaca : DESA

Untuk nilai sec x, cosec x, dan cotan x tinggal dibalik aja :

sec x, merupakan kebalikan dari cos x , sehingga sec x = c/a —> dibaca MISA

cosec x, merupakan kebalikan dari sin x, sehingga cosec x = c/b —> dibaca MIDE

cotan x, merupakan kebalikan dari tan x, sehingga cotan x = a/b —> dibaca SADE

walaupun gambarnya diputar-putar tetap berlaku

hal yang sama, perhatikan gambar berikut :

konsep diatas tetap berlaku, jadi jangan terpengaruh dengan gambar segitiga siku-siku yang diputar-putar, yang perlu diperhatikan adalah, dimana letak sudut x, sehingga dapat ditentukan sisi depan, sisi samping dan sisi miring untuk mendapatkan nilai sin x, cos x dan tanx, begitujuga untuk nilai sec x, cosec x dan cotan x.

Nilai Perbandingan Trigonometri untuk sudut istimewa

Beberapa sudut istimewa yang kali ini kita pelajari adala h 0^o, 30^o, 45^o, 60^o, 90^o.
Berikut ini adalah tabel Perbandingannya:

Nilai perbandingan Trigonometri di berbagai Kuadran

Sistem kuadran pada bidang cartesius terbagi menjadi 4 bagian yang ditetapkan sebagai berikut:

Kuadran I : daerah yang dibatasi oleh sumbu X positif dan sumbu Y positif.
Kuadran II : daerah yang dibatasi oleh sumbu X negatif dan sumbu Y positif.
Kuadran III : daerah yang dibatasi oleh sumbu X negatif dan sumbu Y negatif.
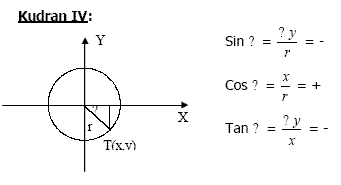
Kuadran IV: daerah yang dibatas i oleh sumbu X positif dan sumbu Y negatif.

Sedangkan nilai perbandingan trigonometri di berbagai kuadran di
atas, dapat dijelaskan dengan gambar berikut ini.

Untuk lebih mempermudah mengingat perbandingan trigonometri dapat dilakukan dengan membaca gambar berikut. Yang positif adalah

»»  READMORE...

KOORDINAT CARTESIUS dan KUTUB

Koordinat cartesius adalah suatu sistem koordinat yang menggunakan dua garis lurus yang saling tegak lurus dan berarah dalam menentukan kedudukan suatu titik pada bidang. Di mana dua garis yang dimaksud adalah sumbu X dan sumbu Y, serta perpotongan kedua titik itu adalah titik asal. Koordinat cartesius sering disebut dengan koordinat sikusiku.
Sedangkan koordinat kutub adalah suatu koordinat yang menggunakan sebuah sinar garis sebagai patokan muka dalam menentukan kedudukan suatu titik pada bidang. Di mana titik pangkal sinar garis itu sebagai kutub atau titik asal dan sinar garis itu sendiri sebagai sumbu kutub.

Untuk Lebih jelas Perhatikan Gambar berikut:

Pada gambar (I) merupakan contoh koordinat cartesius yang menggambarkan kedudukan titik P, sedangkan gambar (II) merupakan contoh koordinat kutub yang menggambarkan kedudukan titik T.

»»  READMORE...

ATURAN SINUS dan COSINUS

Misalkan ?ABC adalah segitiga dengan ? CAB = ? ; ? ABC = ? dan ? BCA = ? serta panjang BC, AC dan AB berturut-turut adalah a, b dan c. Tarik garis melalui titik C di luar garis AB tegak lurus garis tersebut, misal CD.

Tarik garis melalui titik B di luar garis AC tegak lurus garis tersebut, misal BE maka :

Dari (3) dan (6) di dapat:

Mencari Rumus Cosinus

Misalkan ?ABC adalah segitiga dengan ? CAB = ? ; ? ABC = ? dan ? BCA = ? serta panjang BC, AC dan AB berturut-turut adalah a, b dan c. Tarik garis melalui titik C di luar garis AB tegak lurus garis tersebut, misal
CD.

Pandang ? BDC siku-siku di D, maka berlaku teorema phytagoras:

Dengan cara yang sebanding, kita akan memperoleh rumus cosinus yang lain yaitu:

Buktikan sendiri di rumahmu! Rumus Cosinus:

Penggunaan aturan Sinus

Aturan sinus sangat bermanfaat untuk menghitung panjang sisi atau besar sudut pada suatu segitiga.

Contoh 4

a. Diketahui ?? ABC dengan AB = 4 cm, ? CAB = 300 dan ? BCA = 450 Tentukan panjang BC?

Penggunaan aturan Cosinus

Seperti halnya aturan sinus, aturan cosinus sangat bermanfaat untuk menghitung panjang sisi atau besar sudut pada suatu segitiga.

Contoh 5

»»  READMORE...

LUAS SEGITIGA

Luas segitiga adalah banyaknya satuan luas yang tepat menutupi permukaan segitiga itu. Rumus luas segitiga, ada tiga cara yaitu:

Cara I: Luas segitiga = 1/2 x alas x Tinggi; rumus ini dapat digunakan jika salah satu alas dan garis tinggi pada alas tersebut diketahui.

Cara II: Menghitung luas segitiga menggunakan perbandingan trigonometri (Aturan sinus):

Dengan memperhatikan ? B, didapat:

t = BC. Sin A

Sehingga, L ?ABC = 1/2 x AB x BC. Sin A

= 1/2 ca sin A

= 1/2 ac sin A

Dengan memperhatikan ? C, didapat:

t = BC. Sin C

Sehingga, L ?ABC = 1/2 x AC x BC. Sin C

= 1/2 ba sin C

= 1/2 ab sin C

Ketiga rumus luas segitiga di atas dapat digunakan apabila diketahui sebuah sudut dan dua sisi yang mengapit sudut tersebut.

Cara III: Berdasarkan rumus/aturan cosinus yaitu

Rumus luas di atas, dapat digunakan apabila ketiga sisinya diketahui.

»»  READMORE...

Menyusun Rumus Aturan Sinus dan Cosinus

Misalnya siswa sudah tahu pakai rumus aturan sin atau aturan cos. Masalah berikutnya ada sebagian siswa yang masih bingung bagaimana menyusun rumusnya.
Rumus Aturan Sinus pada segitiga ABC adalah:
sin A : BC = sin B : AC = sin C : AB. ….(1)
karena perbandingan maka rumus aturan sinus pada segitiga ABC boleh juga ditulis:
BC : sin A = AC : sin B = AB : sin C. ….(2)
Perhatikan bahwa pada masing masing ruas selalu terdapat nama segitiga tersebut yaitu ABC.
Ruas kiri:
pada persamaan (1) sin A : BC atau pada persamaan (2) BC : sin A.
Ruas tengah:
pada persamaan (1) sin B : AC atau pada persamaan (2) AC : sin B.
Ruas kanan:
pada persamaan (1) sin C : AB atau pada persamaan (2) AB : sin C.
Catatan:
sin A = sin BAC = sin CAB
sin B = sin ABC = sin CBA
sin C = sin ACB = sin BCA
ruas garis AB = BA, AC = CA, dan BC = CB
segitiga ABC = segitiga BAC = segitiga CAB = segitiga BCA = segitiga ACB.
Contoh 1:
Pada segitiga ABC diketahui panjang sisi AB = 8 cm, besar sudut BAC = 60 derajat, dan besar sudut CBA = 75 derajat. Tentukan panjang sisi BC!
Jawab:
Karena diketahui 2 sudut maka gunakan aturan sinus.
Jika ditanya panjang sisi BC maka yang ditulis dahulu diruas kiri adalah BC.
BC : sin A (ingat pada setiap ruas rumus aturan sinus terdapat nama segitiga yang diketahui).
Karena diruas kiri rumus dimulai dengan panjang ruas garis maka di ruas kanan juga dimulai dengan panjang ruas garis. Dalam hal ini AB (karena pada soal diketahui panjang ruas garis AB).
AB : sin C.
BTW yang ada kan cuman sudut BAC = sudut A dan sudut CBA = sudut B.
Besar sudut C kan belum diketahui… Tenang aja ;).
Pada suatu segitiga ABC berlaku:
sudut A + sudut B + sudut C = 180 derajat.
sudut C = 180 derajat - sudut A - sudut B. Bisa ditentukan besar sudut C nya kan.
Jadi rumus aturan sinus yang dipakai adalah BC : sin A = AB : sin C.
Rumus Aturan Cosinus pada segitiga PQR adalah:
(1) PQ kuadrat = PR kuadrat + RQ kuadrat - 2 . PR . RQ . cos R
(2) PR kuadrat = PQ kuadrat + QR kuadrat - 2 . PQ . QR . cos Q
(3) QR kuadrat = QP kuadrat + PR kuadrat - 2 . QP . PR . cos P
Perhatikan bahwa nama garis di ruas kiri dan nama sudut di ruas kanan sesuai dengan nama segitiga tersebut yaitu PQR.
Trus bagaimana dengan ruas kanan?
Bentuk kuadrat diruas kanan diambil dari ruas kiri, caranya adalah menyelipkan huruf dari nama segitiga yang belum ada di ruas kiri.
Pada persamaaan (1) ruas kirinya PQ maka ruas kanannya adalah PR dan RQ.
Pada persamaaan (2) ruas kirinya PR maka ruas kanannya adalah PQ dan QR.
Pada persamaaan (3) ruas kirinya QR maka ruas kanannya adalah QP dan PR.
Contoh 2:
Pada segitiga PQR ditentukan panjang sisi-sisi PQ = 10 cm, PR = 12 cm dan QR = 8 cm. Nilai sin R = ….
Jawab:
Karena tidak ada sudut yang diketahui maka gunakan aturan cosinus!
Karena yang ditanya sudut R maka tulislah pada ruas kiri PQ (ingat garis di ruas kiri dan nama sudut di ruas kanan sesuai dengan nama segitiga PQR).
Bentuk kuadrat diruas kanan adalah dengan menyelipkan huruf yang belum ada pada ruas garis disebelah kiri. Ruas garis disebelah kiri adalah PQ. Dari nama segitiga PQR berarti huruf yang belum di pakai adalah R. Di ruas kanan akan menggunakan panjang ruas garis PR dan RQ.
Jadi rumus aturan cosinus yang digunakan adalah:
PQ kuadrat = PR kuadrat + RQ kuadrat - 2 . PR . RQ . cos R
Yang muncul nanti adalah nilai cos R. Iya dhonk… Kan pakai rumus aturan cosinus. Padahal yang ditanya sin R. Gimana dhonk?
Nah, untuk mendapatkan nilai sin R gunakan pengertian trigonometri. Dalam hal ini kita tidak lagi berbicara tentang segitiga PQR. Sekarang yang kita bicarakan adalah segitiga siku-siku dengan salah satu sudutnya adalah R dan nilai cos R diketahui.
Menurut pengertian trigonometri:
Nilai cosinus suatu sudut = sisi samping : sisi miring.
Anggap nilai cos R yang telah diperoleh sebagai perbandingan sisi samping dan sisi miring.
Jadi sudah diketahui sisi samping dan sisi miring. Yang ditanya sin R.
Nilai sinus suatu sudut = sisi depan : sisi miring.
sisi depan kan belum ada?
Pada suatu segitiga siku-siku berlaku:
sisi depan kuadrat = sisi miring kuadrat - sisi samping kudrat.
Nah sudah ada sisi depan dan sisi miring. Berarti sin R dapat ditentukan.

»»  READMORE...